本篇笔记文档名 👇
•27数学-张宇1000题函数极限强化题1-10✔
本文档为张宇1000题函数极限强化篇（题1-10）的解析笔记，针对考研数学一学生。内容涵盖幂指函数极限（如arcsin x与sin2x的极限计算）、变限积分极限（含积分的极限问题）、泰勒展开与等价无穷小替换（如ln(1+sin2x)~2x的应用）、洛必达法则的灵活使用（分子含变限积分时的求导处理）等。每道题详细分析特征、解题思路及步骤，通过具体例题讲解幂指结构取指对数、等价无穷小替换、复合函数极限处理等技巧，帮助学生掌握函数极限的核心计算方法，提升考研数学极限题型的解题能力。
文档的预览图如下，需要完整PDF文件的同学，文末有文档编码，保存后即可直接打印使用。
📑27数学-张宇1000题函数极限强化题1-10
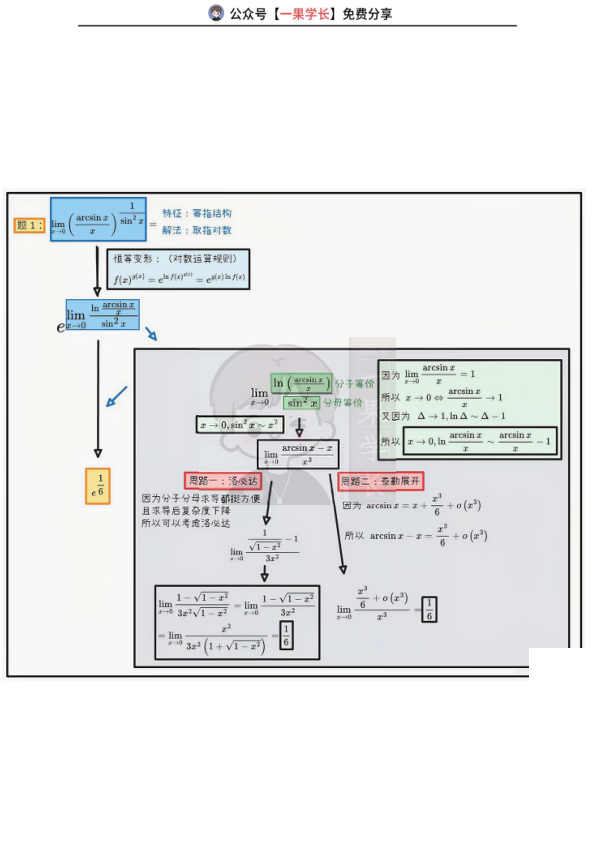
特征:幂指结构 解法:取指对数
恒等变形:f(x)^g(x)=e^{ln f(x)^g(x)}=e^{g(x)ln f(x)}
lim_{x→0} [ln(arcsin x) – ln(sin2x)] / (1/x)？不对，原题是lim_{x→0} (arcsin x)^{sin2x}，分母等价，分子等价，用洛必达或泰勒展开。
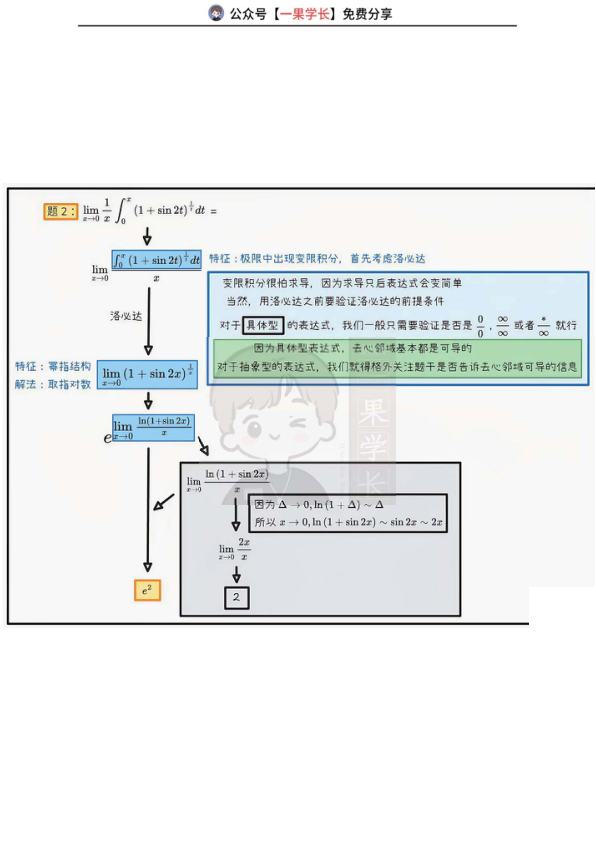
题2: lim_{x→0} (1+sin2x)^{1/x}
特征:幂指结构 解法:取指对数
ln(1+sin2x)~sin2x~2x，指数部分为2x/x=2，极限为e^2。
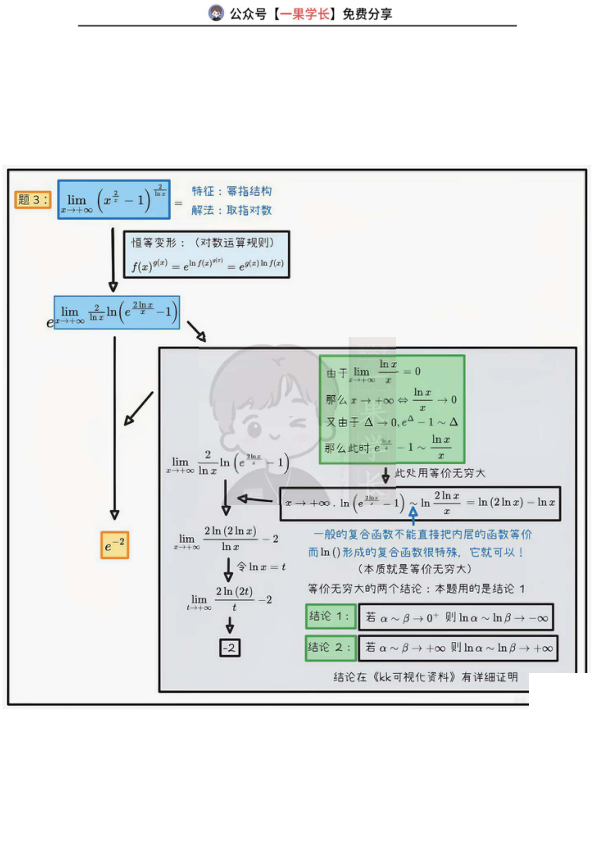
题3: lim_{x→+∞} (x^{2/x} – 1)^{2/ln x}
特征:幂指结构，取指对数后转化为指数函数，令t=lnx，转化为t→+∞，用等价无穷大结论：若α~β→+∞，则lnα~lnβ，简化计算得结果e^{-2}。
题4: 计算lim_{x→0} [∫{0}^{x} (e^{t} – 1) sin t dt] / x^4
分母等价：e^{t} – 1~t，sin t~t，积分后分子为∫0^x t^2 dt = x^3/3，用洛必达法则得lim [ (e^x – 1) sin x ] / (4x^3) = 1/4。
题5: lim{x→0} [1 + 2x + 3x^2 + f(x)/x]^(1/x) = e^5
幂指型，取指对数后转化为指数函数，ln[1+2x+3x^2 + f(x)/x] ~ 2x + 3x^2 + f(x)/x，除以x后极限为2 + lim f(x)/x^2 =5，故lim f(x)/x^2=3，f(x)~3x^2。
题6: 设f(x)在x=3邻域可微，lim_{x→3} f(x)=0，求lim_{x→3} [x∫{x}^{3} f(s)ds]/(3-x)^2
分子分母均为0，用洛必达法则，分子导数为∫{x}^{3} f(s)ds – x f(x)，分母导数为-2(3-x)，再洛一次得lim f’(x)=4016。
题7: f(x),g(x)在x=0邻域连续，x→0时f~g，比较∫{0}^{x} f(t)(1-cos t)dt与∫{0}^{x} t^2 g(t)dt的等价性
用定义法，lim [f(x)(1-cosx)]/[g(x)x^2] = lim [1(x^2/2)]/[1x^2] = 1/2，故同阶非等价。
题8: a∫{0}^{x^2} cos t^2 dt与sinx – b ln(1+x)是等价无穷小，求(a,b)
∫0^{x^2} cos t^2 dt ~ x^2，sinx – b ln(1+x) ~ (1 – b)x + (b/2)x^2，令1 – b=0，b=1，a/(b/2)=1得a=1/2，故(a,b)=(1/2,1)。
题9: ∫{0}^{x}(e^{t cos t^2} – e^t)dt ~ a x^b，求(a,b)
e^{t cos t^2} ~ e^t [1 + t(-t^4/2)]，积分后分子为∫0^x e^t (-t^4/2)dt ~ -x^6/12，故a=-1/12，b=6。
题10: lim_{x→3} (3x^2 + bx^2 + x)/(x + a)=25，求ab
分母x→3时x+a=0→a=-3，分子导数6x + 2bx +1，代入x=3得18 +6b +1=25→b=5，故ab=-15。
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
