27考研周洋鑫等价无穷小速记公式

本文档为数学等价无穷小速记笔记，系统整理常用等价公式及应用方法。包含8个基础等价公式（如sinx~x、ln(1+x)~x等）、4个推导记忆公式（如a^x-1~xlna）、2个重点等价关系（f(x)→1时f(x)-1~lnf(x)）及7个图像记忆结论。同时讲解无穷小量定义（limf(x)=0）、比阶方法、替换准则（乘法可用，加减法需检验）、和取低阶原则（有限个无穷小加减取最低阶），结合例题（如cosx-cos2x与sinx-tanx等价无穷小）强化应用，涵盖高数极限、泰勒公式等相关考点，适合快速记忆与复习。

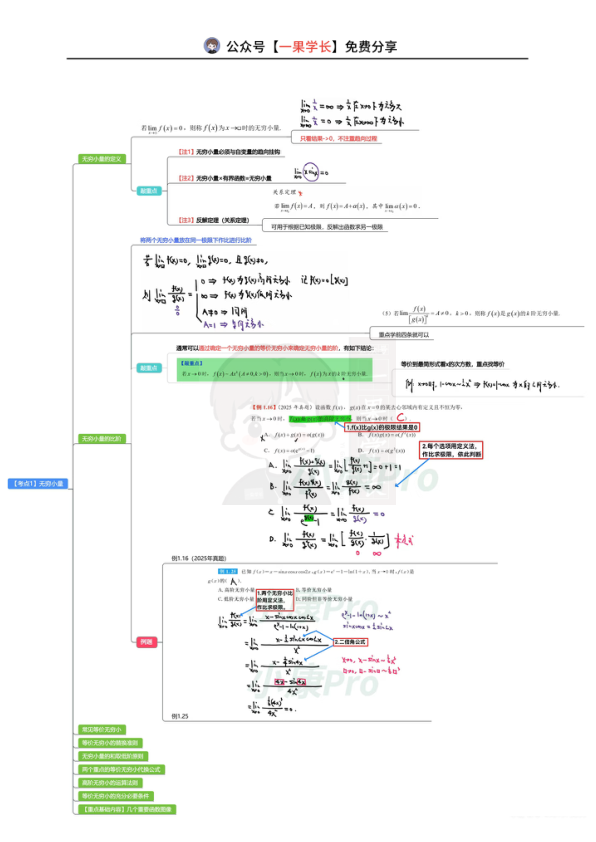
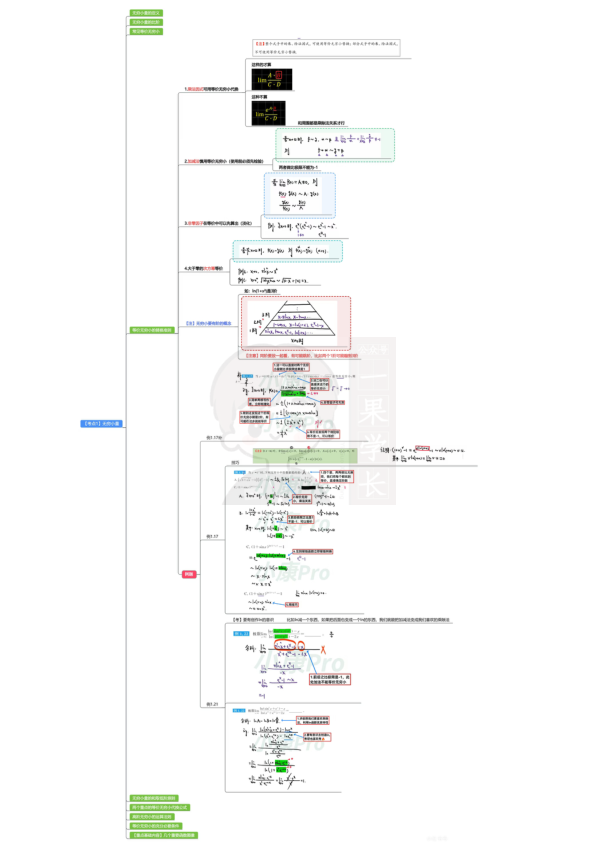
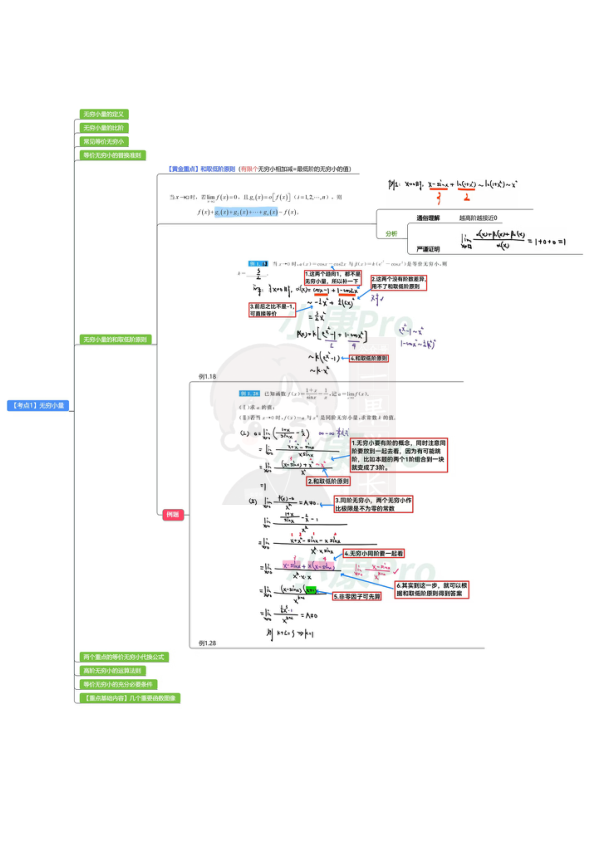
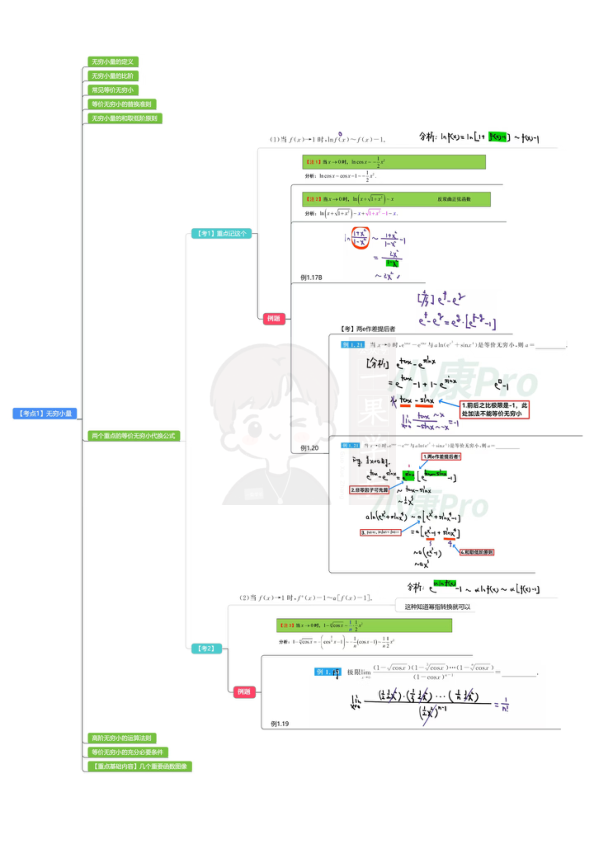
文档的预览图如下，需要完整PDF文件的同学，文末有文档编码，保存后即可直接打印使用。