27考研30讲题型方法：数列极限1（重难点）

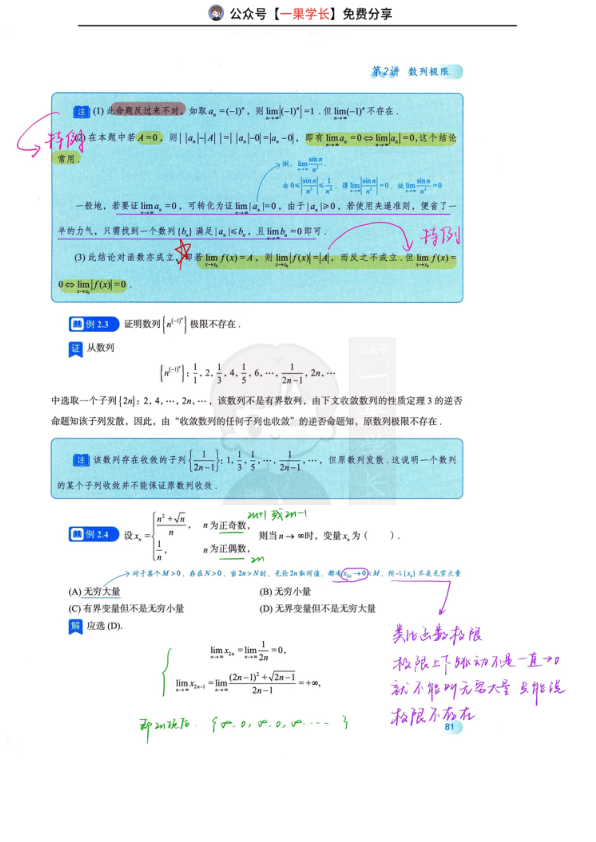
本文档为考研数学基础30讲·高等数学分册中关于数列极限的知识点笔记，涵盖数列极限的定义（ε-N语言）、与函数极限的区别（全局有界性、N的存在性）、收敛数列的核心性质（唯一性、有界性、保号性）、极限四则运算法则，以及通过海涅定理（归结原则）将数列极限转化为函数极限的方法。内容包含典型例题解析，如证明|aₙ|极限等于|A|（三角不等式应用）、判断{n^(-1)^n}极限不存在（子列收敛于不同值）、分析数列aₙ=1-(-1)^n/n的最值（首项最大值、极限收敛性）等，帮助考生系统理解数列极限的概念、收敛性质及解题技巧。

文档的预览图如下，需要完整PDF文件的同学，文末有文档编码，保存后即可直接打印使用。