本篇笔记文档名 👇
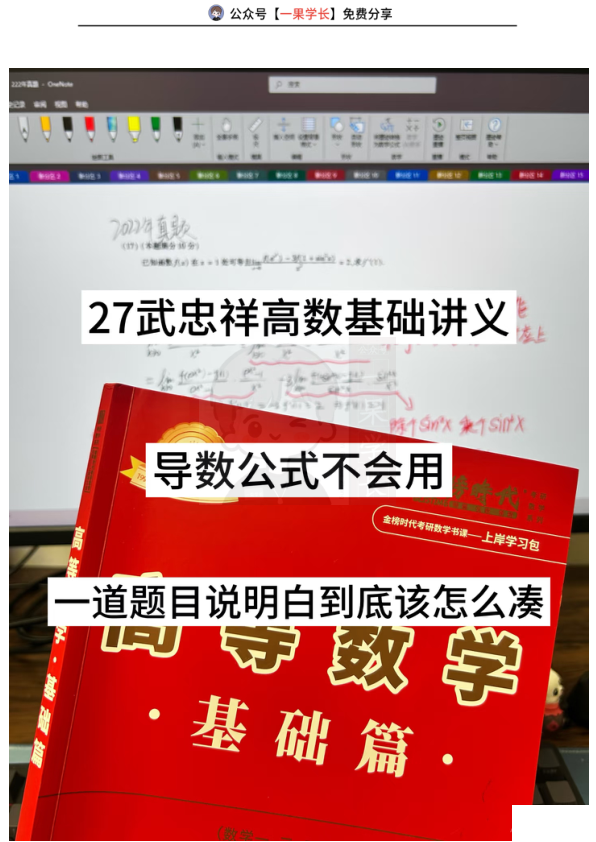
本文档为武忠祥高数基础讲义中导数公式运用的考研数学笔记,核心内容涵盖导数定义(含左导数、右导数)及其等价形式,如f’(x₀)=lim(x→x₀)[f(x)-f(x₀)]/(x-x₀)=lim(h→0)[f(x₀+h)-f(x₀)]/h等。通过2022年考研数学真题(17题)详细解析,演示如何利用极限与等价变形凑导数定义式,解决函数在x=1处可导时f’(1)的计算问题,帮助学习者掌握导数公式的实际应用技巧,适用于考研数学基础阶段对导数概念及应用的复习巩固。
文档的预览图如下,需要完整PDF文件的同学,文末有文档编码,保存后即可直接打印使用。
📑27数学-武忠祥高数基础讲义导数公式运用
导数定义:设函数y=f(x)在x₀的某邻域内有定义,若lim(Δx→0)[f(x₀+Δx)-f(x₀)]/Δx存在,则称f(x)在x₀处可导,极限值为f’(x₀)。常用等价形式:f’(x₀)=lim(x→x₀)[f(x)-f(x₀)]/(x-x₀)=lim(h→0)[f(x₀+h)-f(x₀)]/h。左导数:函数在x₀左邻域有定义,左极限lim(Δx→0⁻)[f(x₀+Δx)-f(x₀)]/Δx存在时,为f’₋(x₀);右导数:右邻域定义,右极限存在时为f’₊(x₀)。2022年真题(17题):已知f(x)在x=1处可导,且lim(x→0)[f(eˣ²)-3f(1+sin²x)]/x²=2,求f’(1)。解题关键:利用等价无穷小替换(eˣ²-1~x²,sin²x~x²),将原式拆分为两项:lim(x→0)[f(eˣ²)-f(1)]/(eˣ²-1)·(eˣ²-1)/x² – 3lim(x→0)[f(1+sin²x)-f(1)]/(sin²x)·(sin²x)/x²。代入等价无穷小后,第一项为f’(1)·1,第二项为3f’(1)·1,整体得f’(1)-3f’(1)=-2f’(1)=2,解得f’(1)=-1。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。