本篇笔记文档名 👇
•27数学-周洋鑫线代两大特殊矩阵总结✔
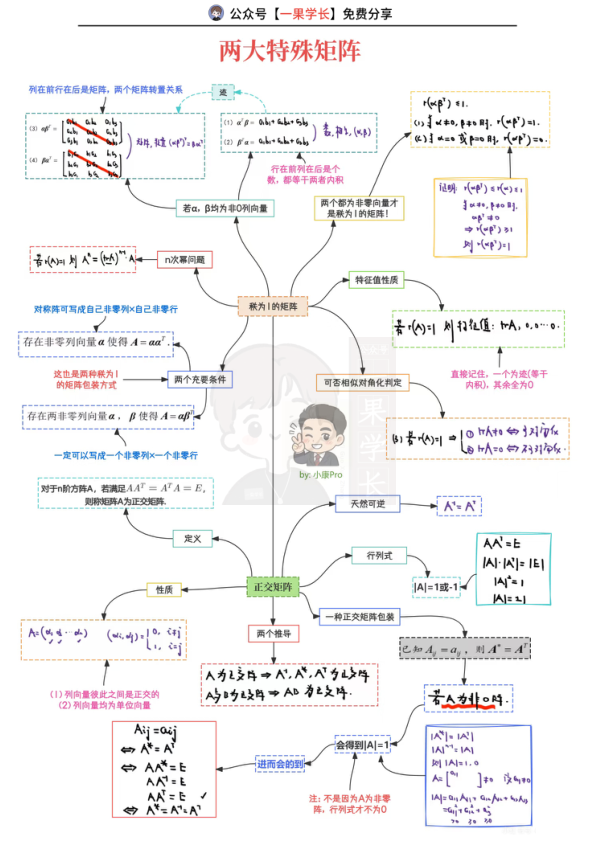
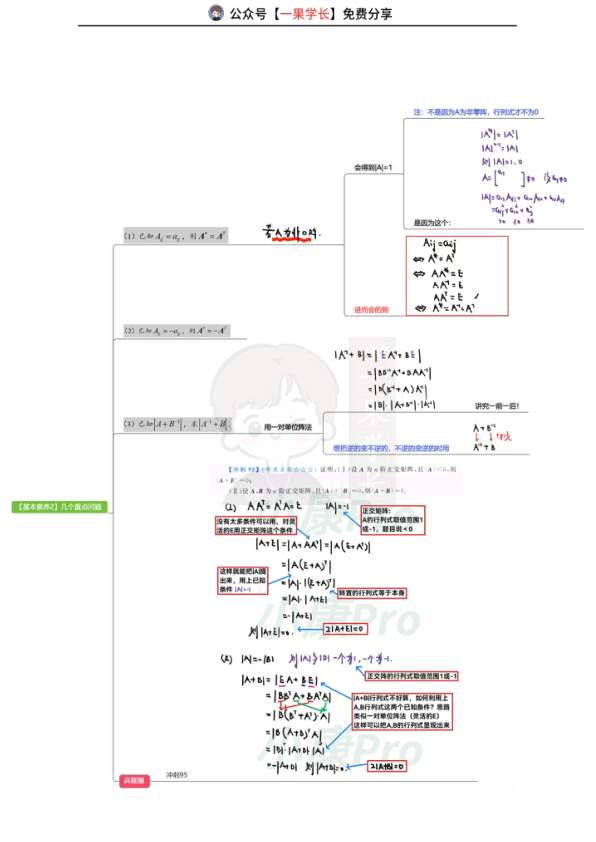
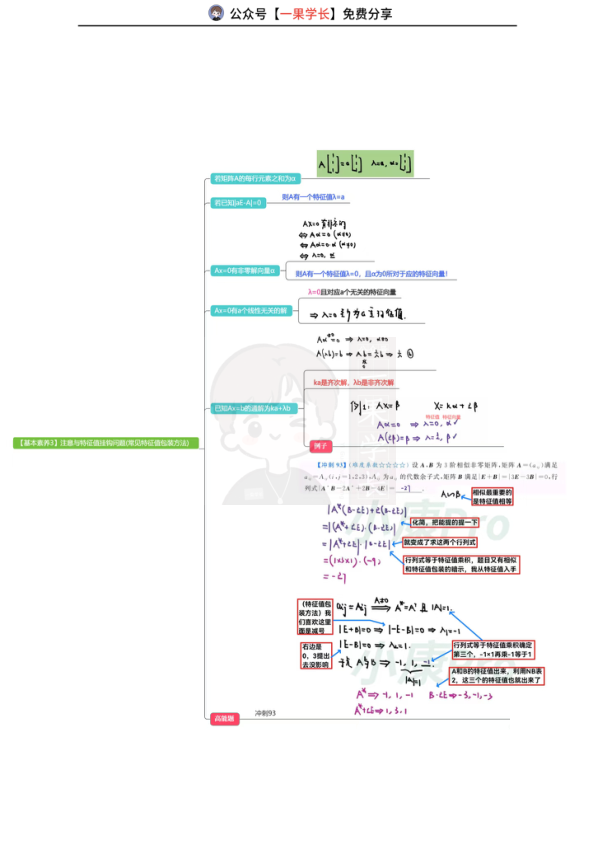
本文档为周洋鑫线代课程中关于两大特殊矩阵（正交矩阵和秩为1矩阵）的总结笔记。内容涵盖矩阵定义、性质（如秩为1矩阵可表示为非零列向量与非零行向量的乘积）、特征值与行列式计算（利用特征值乘积求行列式）、相似对角化判定方法，以及相关定理（如正交矩阵满足AAT=E，行列式为±1）。包含行列式乘法定理、拉普拉斯行列式、特征值性质等核心知识点，并通过例题（如已知特征值求行列式、正交矩阵行列式关系）讲解应用技巧，适合考研线性代数复习使用。
文档的预览图如下，需要完整PDF文件的同学，文末有文档编码，保存后即可直接打印使用。
📑27数学-周洋鑫线代两大特殊矩阵总结
行列式计算：基本性质|A^T|=|A|，|AB|=|A||B|，|kA|=k^n|A|，|A^{-1}|=1/|A|，|A^*|=|A|^{n-1}（n≥2）；拉普拉斯行列式公式（分块矩阵）；特征值乘积|A|=λ1λ2…λn。
例题解析：冲刺94题已知A特征值2,3,-1，矩阵B满足A²+2AB+A-B=E，求|A²+BA|，利用特征值乘积化简得结果-48；强化17题正交矩阵|A|=-1，证|A+E|=0，结合A^T A=E推导得证。
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
