
本篇笔记文档名 👇

•27数学-武忠祥洛必达求极限总结✔
本文档为27数学-武忠祥洛必达求极限总结,属于考研数学武忠祥系列笔记。内容涵盖洛必达法则的基本定义、适用类型及注意事项,详细讲解了0/0型、∞/∞型、∞-∞型、0·∞型(含1^∞、∞^0、0^0)等未定型极限的转化方法与解题步骤。通过典型例题(如lim(x→1)lncos(x-1)/(1-sin(πx/2))、lim(x→+∞)(x+√(1+x²))^(1/x)等)展示洛必达法则的实际应用,包含等价无穷小代换、取对数、转化未定型等技巧,帮助考生系统掌握洛必达求极限的核心方法与易错点,适合考研数学备考复习使用。
文档的预览图如下,需要完整PDF文件的同学,文末有文档编码,保存后即可直接打印使用。

📑27数学-武忠祥洛必达求极限总结
一、洛必达法则
若1) $\lim {x \to x{0}} f(x)=\lim {x \to x{0}} g(x)=0(\infty)$;
2) $f(x)$ 和 $g(x)$ 在 $x_{0}$ 的某去心邻域内可导,且 $g'(x) \neq 0$;
3) $\lim {x \to x{0}} \frac{f'(x)}{g'(x)}$ 存在(或为无穷大),则 $\lim {x \to x{0}} \frac{f(x)}{g(x)}=\lim {x \to x{0}} \frac{f'(x)}{g'(x)}$。
二、适用类型
1. 转化框图:
$\frac{0}{0}, \frac{\infty}{\infty} \Leftarrow \begin{cases} 0 \cdot \infty \Leftarrow \begin{cases} 1^{\infty} \ \infty^{0} \ 0^{0} \end{cases} \ \infty – \infty \end{cases}$
- 注意问题:
- 使用前检验条件是否满足;
- 若仍为未定型且条件满足,可重复使用;
- 含极限非零因子可单独求极限;
- 结合等价无穷小或恒等变形简化运算。
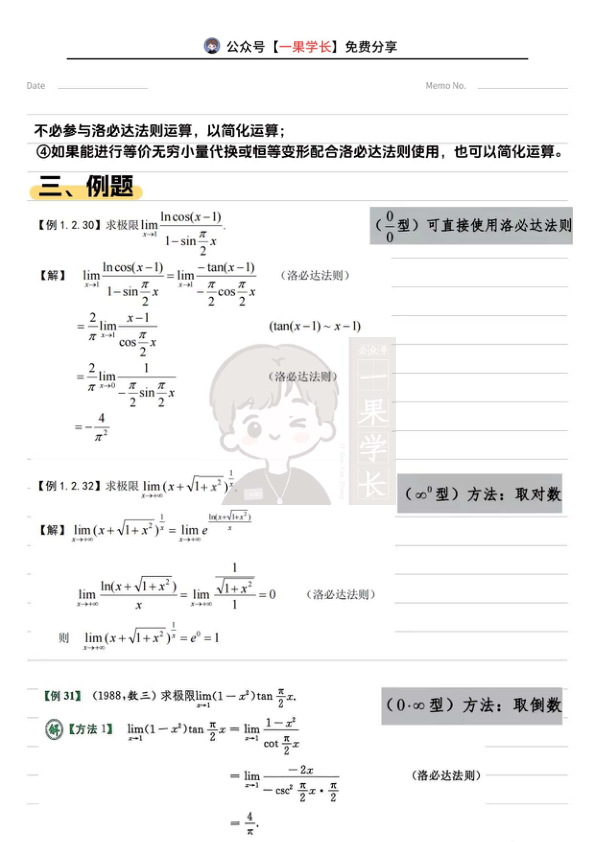
三、例题
1. $\lim {x \to 1} \frac{\ln \cos (x-1)}{1 – \sin \frac{\pi}{2} x}$(0/0型):直接用洛必达法则,得解为 $-\frac{4}{\pi^2}$。
2. $\lim {x \to +\infty}(x + \sqrt{1 + x^2})^{\frac{1}{x}}$(∞⁰型):取对数后用洛必达法则,得解为1。
3. $\lim _{x \to 1}(1 – x^2) \tan \frac{\pi}{2} x$(0·∞型):转化为0/0型,用洛必达法则,得解为 $\frac{4}{\pi}$。
