本篇笔记文档名 👇
•27数学-武老师《高数基础篇》1-5章公式总结✔
武老师《高数基础篇》1-5章高数公式总结,涵盖常用等价无穷小、基本求导公式(含莱布尼兹公式、复合函数、反函数、隐函数、参数方程求导)、麦克劳林公式、渐近线与曲率半径、积分公式(基本积分、变限积分、定积分结论、反常积分敛散性)等核心知识点,系统梳理高数基础公式及应用方法,为考研数学复习提供全面参考,助力学生夯实基础、提升解题能力。
文档的预览图如下,需要完整PDF文件的同学,文末有文档编码,保存后即可直接打印使用。
📑27数学-武老师《高数基础篇》1-5章公式总结
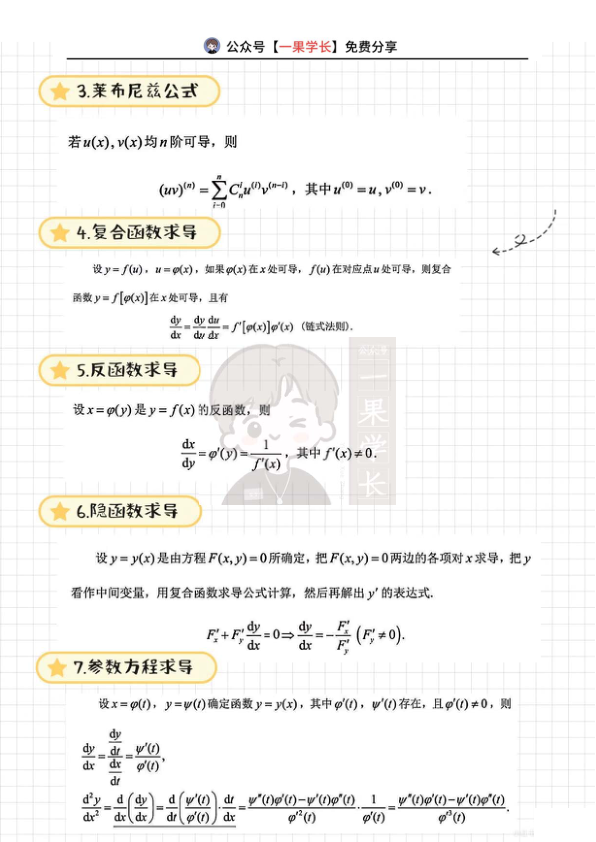
武老师《高数基础篇》1-5章高数公式总结,内容包括:1.常用等价无穷小:当x→0时,sinx~tanx~arcsinx~arctanx~e^x-1~ln(1+x)~x;a^x-1~xln a;1-cosx~(1/2)x²;(1+x)^a-1~ax等。2.基本求导公式:常数导数为0;(sinx)’=cosx;(tanx)’=sec²x;(a^x)’=a^x ln a;(log_a x)’=1/(x ln a);(arcsinx)’=1/√(1-x²)等。3.莱布尼兹公式:若u(x)、v(x)均n阶可导,则(uv)^(n)=ΣC(n,i)u^(i)v^(n-i)。4.复合函数求导:设y=f(u),u=φ(x),则dy/dx=f’[φ(x)]φ’(x)(链式法则)。5.麦克劳林公式:e^x=1+x+x²/2!+…+x^n/n!+o(x^n);sinx=x-x³/3!+…+(-1)^n x^(2n+1)/(2n+1)!+o(x^(2n+1))等。6.积分公式:∫x^k dx=x^(k+1)/(k+1)+C(k≠-1);∫1/x dx=ln|x|+C;∫cosx dx=sinx+C等。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。