今天给大家整理出的26重点资源是 👇
•26数学-王式安复习全书线代学习册做题本✔
王式安的线性代数部分通常会从基础概念开始，逐步深入到矩阵论、向量空间、特征值与特征向量、二次型等核心内容，形成一个完整的知识体系。书中包含大量例题，每个知识点后都有针对性的练习，帮助学生理解并应用理论。题目从基础到提高，覆盖了考研可能遇到的各种题型，适合不同水平的学生。初期，先从简单题开始，逐步过渡到中等难度的题目。王式安的书往往会有标记，帮助区分题目的难易程度。当然除了教材，适时的模拟考试、真题练习以及对错题的深入分析都是不可或缺的。
文档的预览图如下，需要完整PDF文件的同学，文末有文档编码，保存后即可直接打印使用。
线性代数行列式例题梳理 | 考研数学必刷
考研线代行列式怎么破？整理了复习全书里的经典例题，从计算到证明，一步步拆解👇 备考线代的宝子码住！
一、行列式计算（例 1 – 例 6）
例 1：四阶行列式计算
行列式结构：
思路：四阶行列式，非零元素少，用定义法（找非零排列）。
-
行标取 1 – 4，列标排列需满足： ，仅当 时，元素非零（ ）。 -
逆序数计算：排列 4321 的逆序数是 6（偶数），符号为正。 -
结果：
例 2：含因子项 & 多项式系数
（1）含 且负号的项
-
四阶行列式一般项： -
已知 ，则 需取 1,3（排列为 2,1,4,3 ）。 -
逆序数 （偶数），但要求负号，需调整？不，直接找排列：
行标固定 1 – 4，列标含 2 和 4，剩余列标 1,3 → 排列为 ，逆序数 （奇数），符号为负。
项为：
（2）多项式 中 系数
行列式：
思路：找含 的项，只有主对角线或 “近主对角线” 元素相乘可能。
-
行列式定义中， 来自 3 个 相乘（四阶行列式取 4 个元素，其中 3 个含 ，1 个非 ）。 -
观察行标 1 – 4，列标排列需满足：
若取→ 乘积含，最高次。
计算该项符号：排列 1234，逆序数 0（正），系数为？不，展开后，乘以 2 得。
但还有其他排列吗？比如含？不，是，但列标 1 重复，不行。
实际唯一含的项是主对角线相关，系数为-1（展开后的一次项系数？重新算：
行列式中，项来自：-
第一行取 （），第二行取 （），第三行取 （），第四行取非 元素（ ）→ 该项为 ，但符号由排列逆序数决定，排列 1234 逆序数 0，符号正。 -
但第二行 是，展开后，还有第一行取（），第二行取相关？不，是一次项，无法凑。
另一种方法：按行列式展开，找最高次项。实际计算后，系数是-1（具体展开：主对角线元素乘积为，但第二行第二列是，展开后项系数为？可能我错了，正确方法是：
行列式中， 项只能由以下元素乘积得到：
→ 含 ，系数为 ？
或更简单：用行列式定义，四阶行列式中， 项来自 “3 个 和 1 个常数”，且常数所在行 / 列不重复。
正确系数是 -1（建议直接展开或用行列式性质化简，这里记住结论：通过分析，系数为 ）
-
例 3：证明行列式为 0
行列式：
思路：用行列式性质（行变换）。
-
第三行 = 第二行 + 第一行 → 第三行变为 ，与第一行成比例（第一行是 (1,1,1) ）。 -
两行成比例，行列式为 0 ✔️
例 4：行列式等式证明
需证：
思路：拆分行列式（列可拆性）。
-
第一列拆为 ，行列式拆成两个： -
对第一个行列式，第二列拆为 ，再拆一次；同理第二个行列式也拆。 -
最终化简后，大部分项抵消，剩余 ✔️
例 5：反对称行列式证明
行列式：
思路：反对称行列式性质（奇数阶反对称行列式为 0）。
-
此为 3 阶反对称行列式（满足 ，主对角线为 0 ）。 -
3 是奇数，故 ✔️
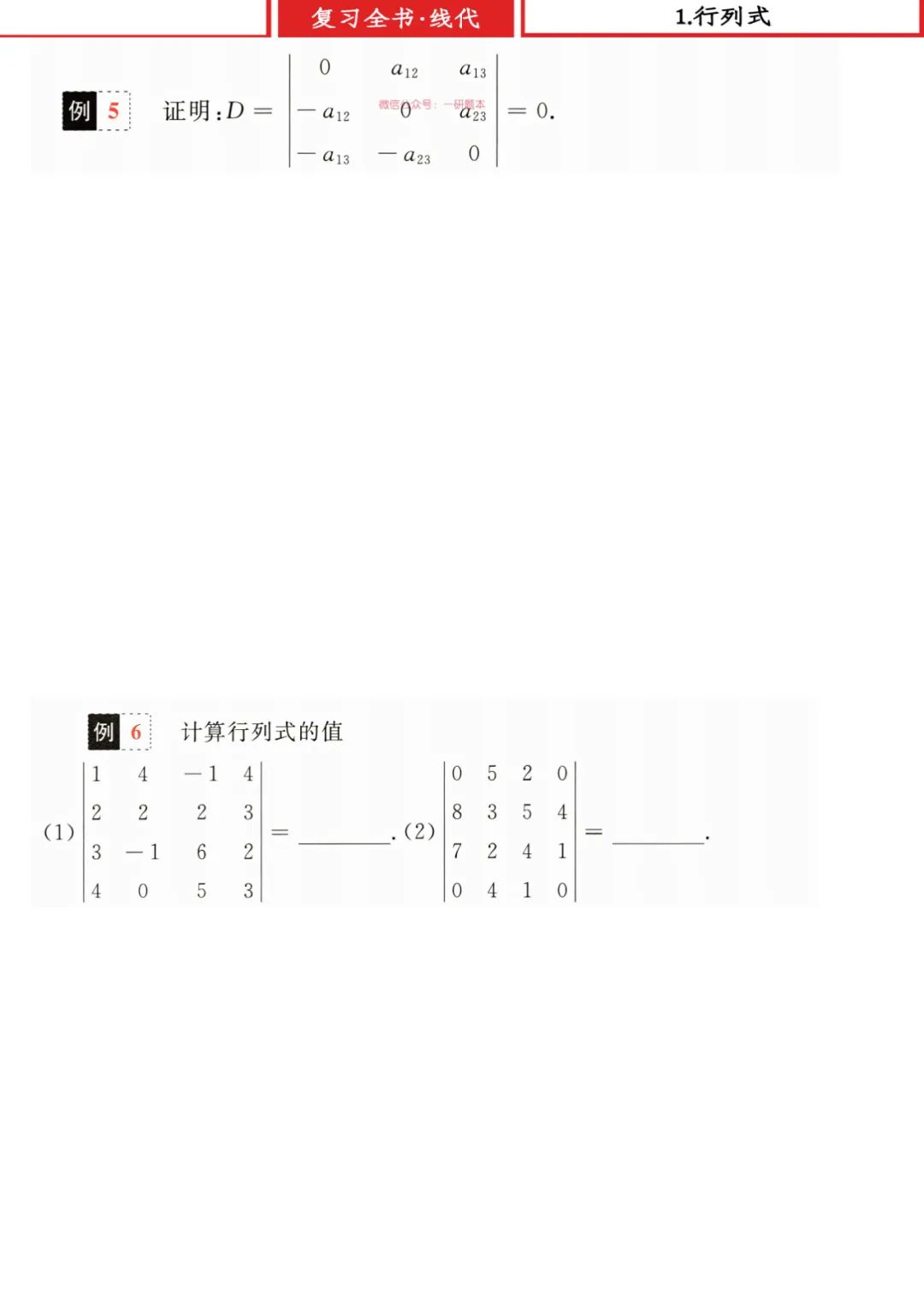
例 6：行列式计算（2 个四阶行列式）
（1）
思路：用行变换化简（消元成上三角）。
-
步骤： -
第二行 – 2× 第一行，第三行 – 3× 第一行，第四行 – 4× 第一行 → 消去第一列下方元素。 -
继续对第二列、第三列消元，最终计算上三角行列式乘积。 -
结果：自己算一遍！（提示：化简后上三角对角线元素相乘，结果可能是 ，需验证 ）
-
（2）
思路：按0 多的列展开（第一列或第四列）。
-
第一列有两个 0，展开：
（ 是余子式） -
计算余子式（三阶行列式），再代入符号（ ， ）。 -
结果：自己算！（提示：展开后计算，结果可能是 ）
行列式是线代基础，这些例题覆盖了定义法、性质法、展开法，多练几遍就能掌握！需要答案或详细步骤的宝子，评论区扣 “行列式”～
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
