今天给大家整理出的26重点资源是 👇
•26数学-线性代数导图✔
线性代数的概览思维导图，可以帮助理解和复习该学科的关键概念。例如：线性方程组、特征值与特征向量、线性变换、行列式、二次型与对称矩阵等。每个部分都可以进一步细化，例如在“矩阵”部分，可以包括矩阵的秩、逆矩阵的求解方法等；在“线性变换”部分，可以探讨变换的不变量和空间的维度理论。使用思维导图时，通过图形和层次结构来组织这些概念，可以帮助记忆和理解它们之间的关系，从而更有效地学习线性代数。
文档的预览图如下，需要完整PDF文件的同学，文末有文档编码，保存后即可直接打印使用。
🧮线性代数行列式考点超全梳理！考研数学必看
考研数学线性代数里，行列式可是基础又重要的考点！这两张思维导图把行列式知识点、题型全总结啦，速码💨
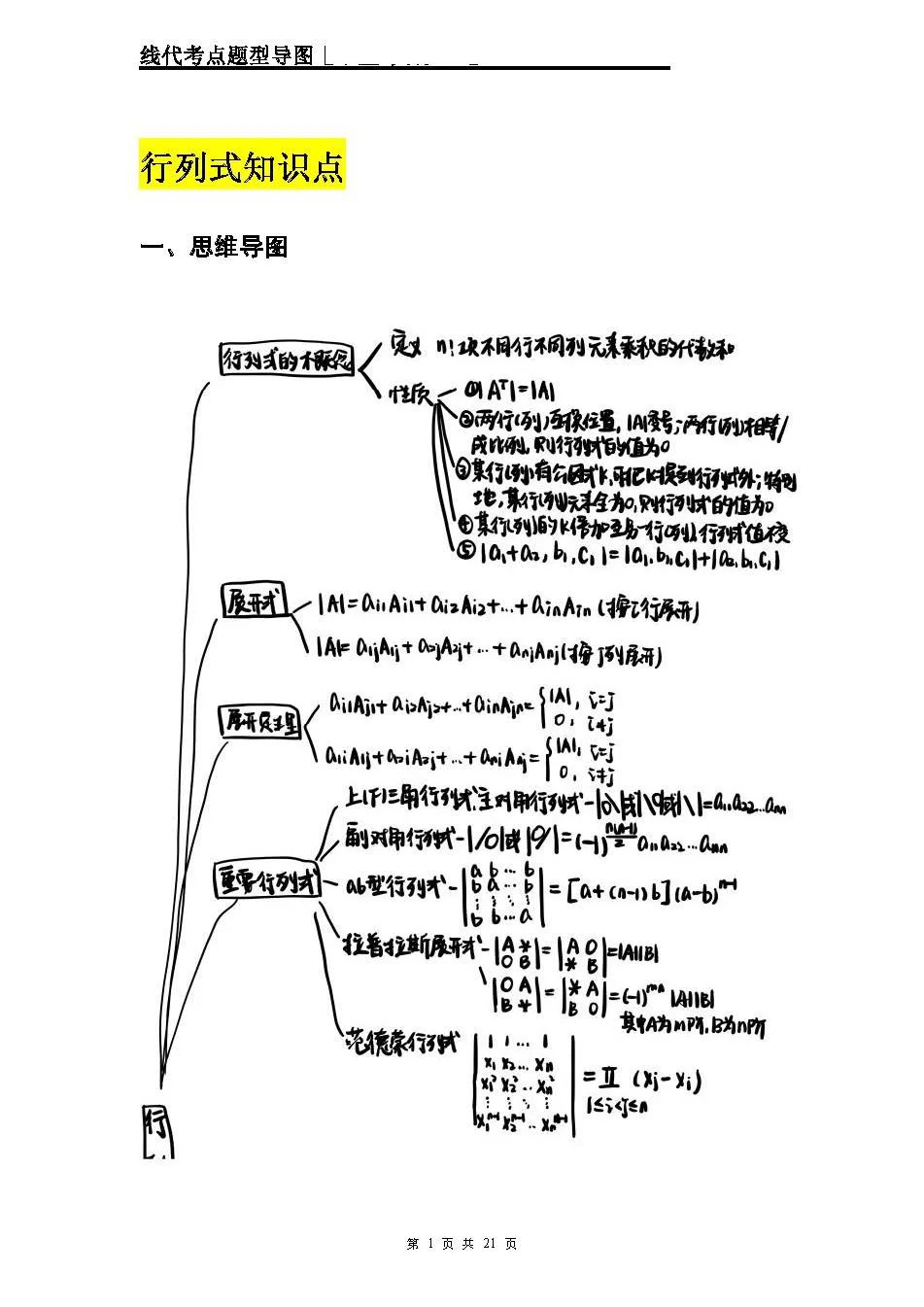
一、行列式知识点框架
（一）行列式的概念
-
定义：n 阶行列式是取不同行不同列元素乘积的代数和，理解 “不同行不同列” 是关键 -
性质：转置行列式值不变（|A^T|=|A| ）；两行（列）互换位置，行列式变号（可用于化简 ）；某行（列）全为 0，行列式为 0 等，还有行（列）加减、数乘等操作对行列式值的影响，这些性质是计算行列式的 “工具包” 🛠️
（二）展开式
-
按行展开：|A|=aᵢ₁Aᵢ₁ + aᵢ₂Aᵢ₂ + … + aᵢₙAᵢₙ （i 行展开） -
按列展开：|A|=a₁ⱼA₁ⱼ + a₂ⱼA₂ⱼ + … + aₙⱼAₙⱼ （j 列展开） -
展开定理：对应元素与代数余子式乘积和，不同行（列）元素与代数余子式乘积和为 0，计算时善用展开简化行列式
（三）重要行列式
-
上下三角行列式：主对角线元素乘积就是行列式值，简单又好算 -
副对角线行列式：值为 (-1)^[n (n – 1)/2] 乘以主对角线元素乘积 -
ab 型行列式、拉普拉斯展开式、范德蒙德行列式等，记住公式直接套，解题效率拉满✨
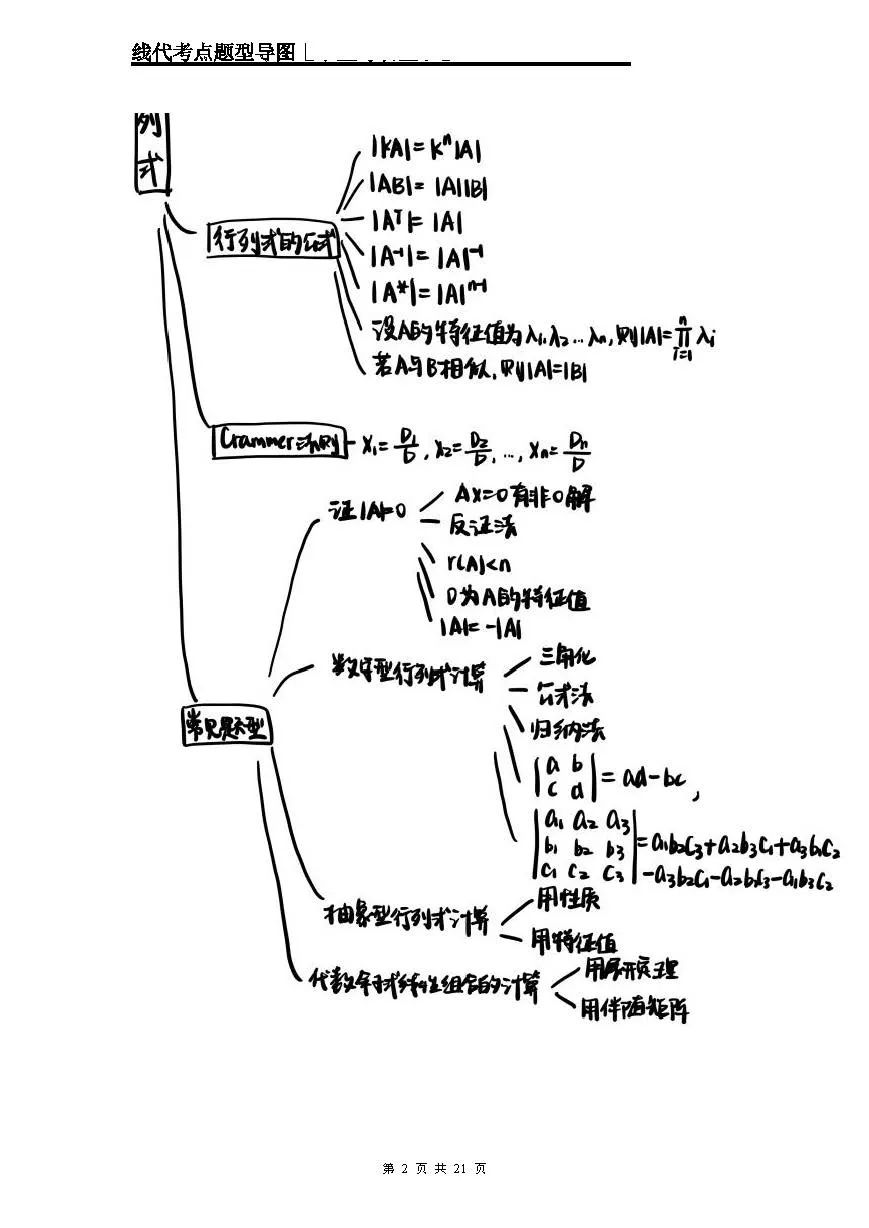
二、行列式题型与方法
（一）行列式的计算
-
公式：|kA|=kⁿ|A| 、|AB|=|A||B| 、|A^T|=|A| 等，熟练运用这些公式化简 -
特殊关系：比如 A 可逆时 |A⁻¹|=|A|⁻¹ ，伴随矩阵 |A*|=|A|ⁿ⁻¹ ，还有特征值与行列式的联系（|A|=λ₁λ₂…λₙ ）
（二）Cramer 法则
用于解线性方程组，xᵢ=Dᵢ/D （D 是系数行列式，Dᵢ 是替换后的行列式 ），前提是 D≠0 才有唯一解
（三）常见题型
-
证 |A|≠0：可通过 Ax=0 只有零解、秩 r (A)=n、0 不是特征值等方法证明 -
数字型行列式计算：三角化、公式法、归纳法等，把复杂行列式转化为熟悉形式 -
抽象型行列式计算：用性质、特征值、展开定理、伴随矩阵等，结合已知条件找关系 -
代数和计算：涉及行列式按行（列）展开的灵活运用，抓住元素与代数余子式的关联
掌握这些，行列式题型基本就能拿下！考研线代复习从基础内容抓起，行列式学好了，后面矩阵、方程组等内容也更顺～
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
