今天给大家整理出的26重点资源是 👇
•26数学-基础阶段高数笔记✔
在高等数学的基础阶段，第一章通常涵盖函数、极限与连续性等核心概念，这些是整个微积分学习的基石。学习第一章时，重点在于理解概念，掌握极限的计算方法，并能灵活应用这些理论解决实际问题。通过做题实践，加深对这些基础概念的理解，为后续章节的学习打下坚实的基础。
文档的预览图如下，需要完整PDF文件的同学，文末有文档编码，保存后即可直接打印使用。
📘高数极限笔记 | 三大定义 + 经典例题，吃透极限基础
高数里极限概念超重要但难理解？整理了手写笔记里的数列极限（ε-N）、函数极限（ε-δ、ε-X） 定义 + 例题，帮你啃透基础📚
一、极限定义分类
1. 数列极限（ε-N 定义）
🌰 核心：对任意 ε>0，存在 N>0，当 n>N 时，|aₙ – A| < ε
理解：只要 n 足够大（超过 N），数列 aₙ 与 A 的距离能无限小，就说 aₙ 极限是 A
2. 函数极限（ε-δ 定义，x→a 时）
🌰 核心：对任意 ε>0，存在 δ>0，当 0<|x – a| < δ 时，|f (x) – A| < ε
👉 注意 “0<|x – a|”：x 趋近 a 但≠a，极限与 f (a) 无关！
👉 例题：
（x→1 时 x≠1，可约分） -
左右极限：x→a⁺（右极限）、x→a⁻（左极限），极限存在 ⇨ 左右极限都存在且相等
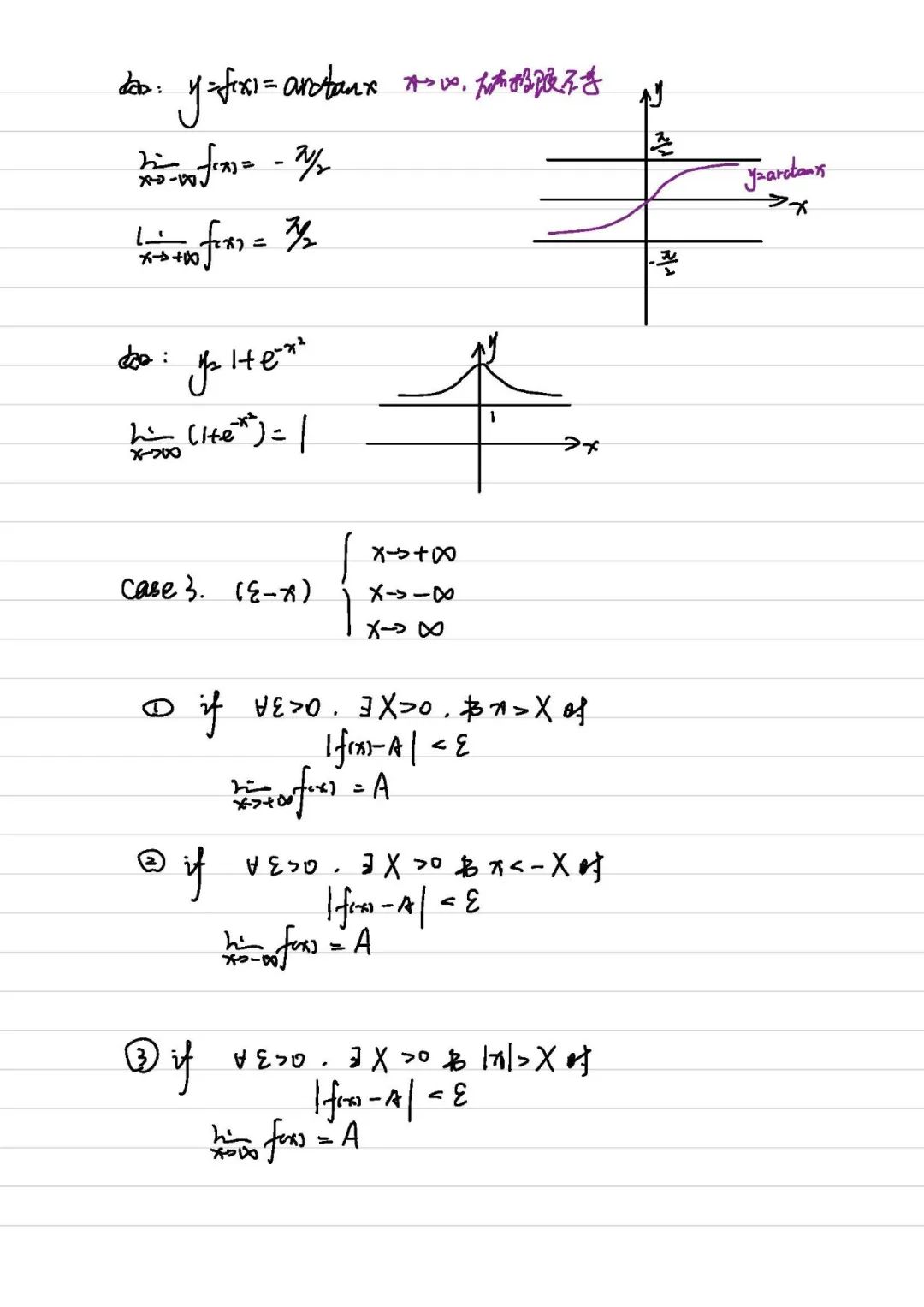
3. 函数极限（ε-X 定义，x→∞ 时）
分三种情况：x→+∞、x→-∞、x→∞，核心都是 “x 绝对值足够大时，f (x) 与 A 距离无限小”
🌰 例题：
：x→-∞ 时极限 -π/2；x→+∞ 时极限 π/2（图像渐近线）
（x→∞ 时 e⁻ˣ²→0 ）
二、关键结论
-
函数极限存在 ⇨ 左右极限都存在且相等 -
若某一侧极限不存在，或左右极限不相等 ⇨ 函数在该点极限不存在
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
