本篇笔记文档名 👇
该文档为高等数学学习笔记,主要涵盖函数极限与连续、一元函数微分学和中值定理三大核心内容。详细记录了等价无穷小替换公式、泰勒展开公式及其应用原则,包括常见函数的泰勒展开式。系统整理了导数定义、微分概念、基本求导公式、复合函数求导法则、参数方程求导方法以及高阶导数的莱布尼茨公式。同时包含了函数几何应用的相关知识,如切线法线方程、极值判定条件、单调性分析、凹凸性判断和拐点识别方法,以及各类渐近线的求解方式。最后阐述了中值定理体系,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒中值定理等重要定理内容。
文档的预览图如下,需要完整PDF文件的同学,文末有文档编码,保存后即可直接打印使用。
📑27数学-小谭数学公式(极限-中值定理)
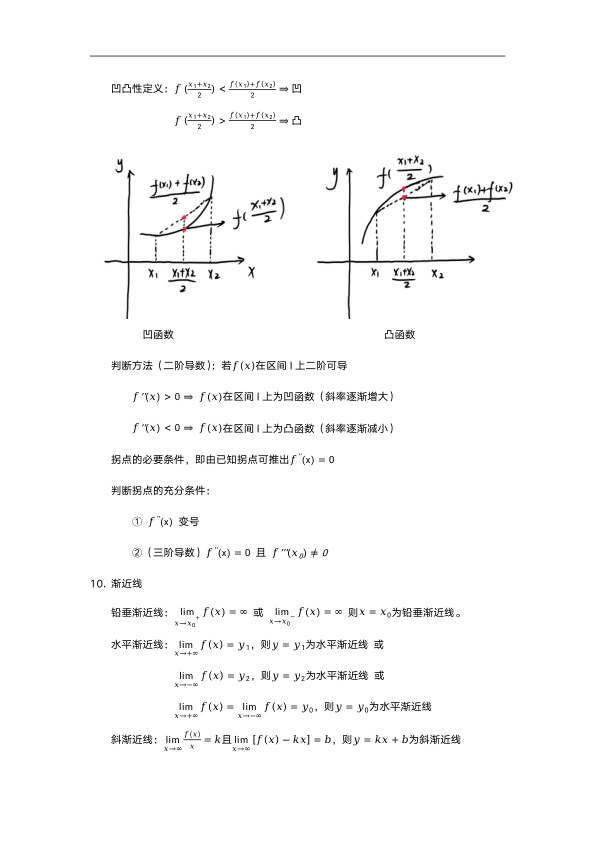
函数极限与连续部分包含等价无穷小公式:当x趋近于0时,sinx~x,tanx~x,arcsinx~x,arctanx~x,1-cosx~1/2x²,e^x-1~x,a^x-1~xlna,(1+x)^a-1~ax,ln(1+x)~x。泰勒公式部分提供了常见函数的展开式:e^x=1+x+x²/2!+…+x^n/n!+…,sinx=x-x³/3!+…+(-1)^n x^(2n+1)/(2n+1)!+…,cosx=1-x²/2!+…+(-1)^n x^(2n)/(2n)!+…,ln(1+x)=x-x²/2+…+(-1)^(n-1)x^n/n+…,1/(1-x)=1+x+x²+…+x^n+…,1/(1+x)=1-x+x²-…+(-1)^n x^n+…。还包括夹逼准则、间断点分类(跳跃间断点、可去间断点、第二类间断点)等极限相关概念。一元函数微分学部分详细列出了导数定义、微分定义、基本求导公式、复合函数求导法则、参数方程求导方法和高阶导数的莱布尼茨公式。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。