今天给大家整理出的26重点资源是 👇
本文档为线性代数学习笔记,系统梳理核心知识点。涵盖行列式部分,包括余子式、代数余子式的定义,行列式的基本性质(如转置行列式值不变,某行有公因式可提出,两行互换变号,行元素为和可拆行列式,行倍加不变等)及计算方法(化为三角行列式、按行/列展开、递推法等),同时提及特征值与行列式的关系、可逆矩阵和伴随矩阵的行列式性质。第三章重点讲解向量组,涉及线性表示(充要条件、表示定理)、线性相关性(充要条件、推论)、线性无关性(充要条件)、向量组的秩与极大无关组,以及n维向量空间的基底、坐标、过渡矩阵等内容,帮助学习者构建知识体系,巩固学习重点。
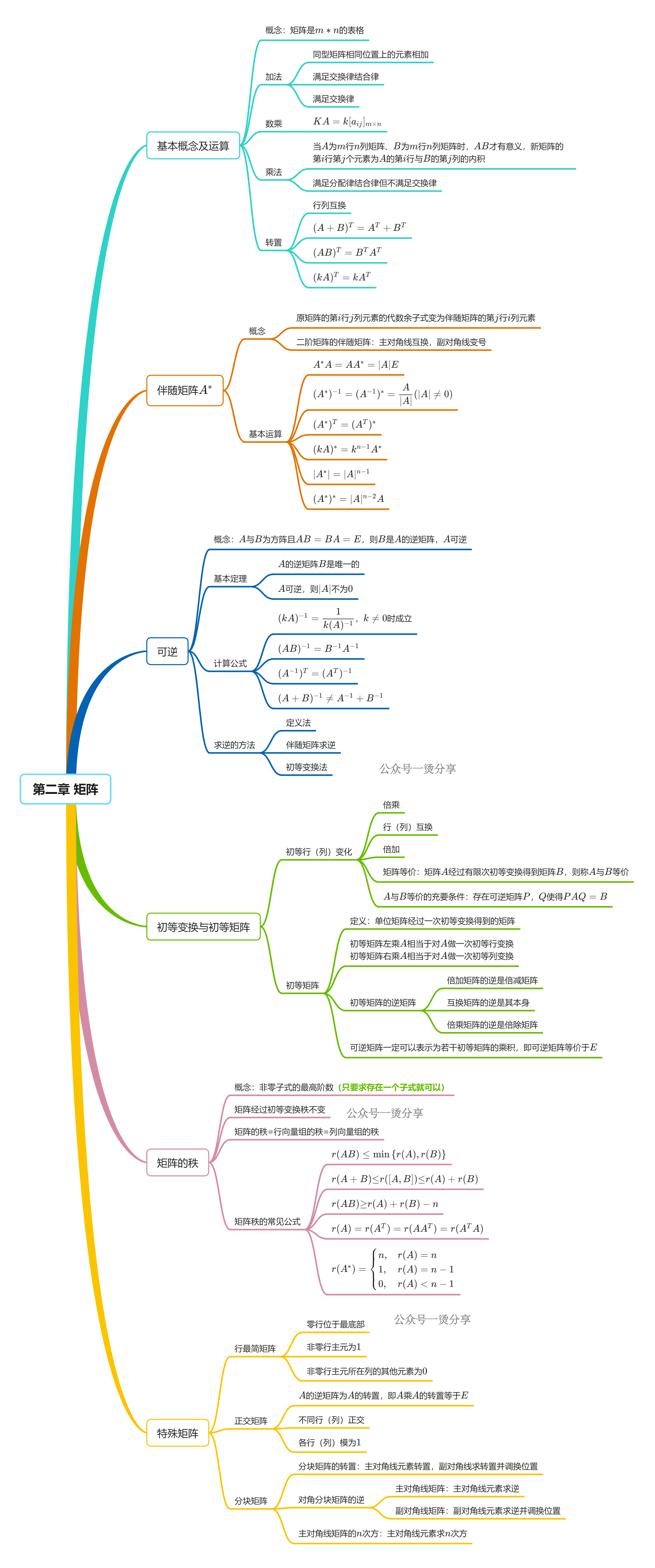
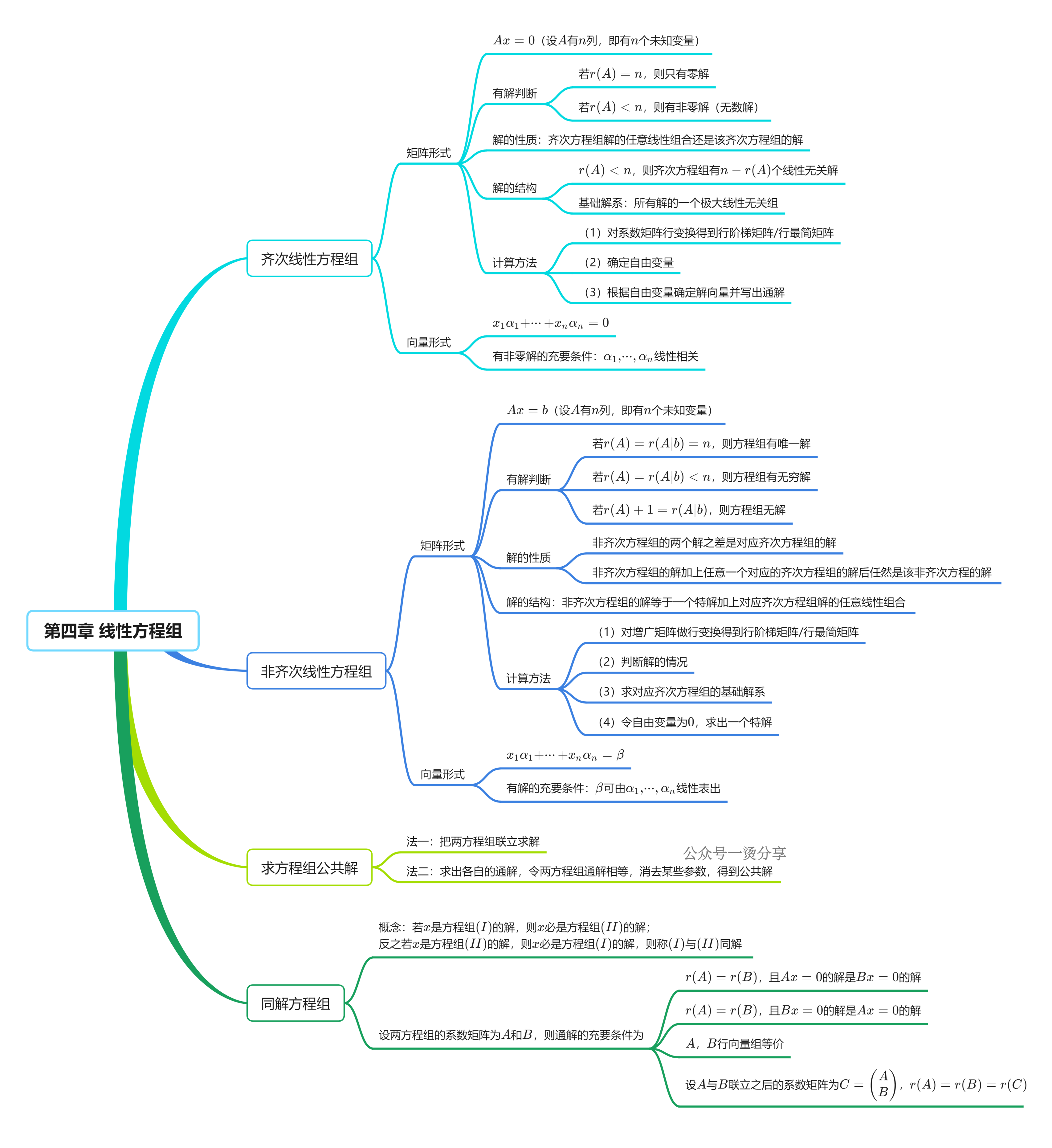
文档的预览图如下,需要完整PDF文件的同学,文末有文档编码,保存后即可直接打印使用。
📚26数学-线性代数导图(一烫)📚
行列式:余子式M为划去aij所在行和列,剩下元素按原位置排列的行列式;代数余子式Aij=(-1)^(i+j)Mij。行列式性质:|A^T|=|A|;某行(列)有公因式k可提到行列式外;某行(列)全为0,行列式值为0;两行(列)互换,行列式变号;两行相等或成比例,行列式为0;某行元素为两数和,可拆为两个行列式之和;某行k倍加至另一行,行列式值不变。kA行列式值=k^n|A|;|AB|=|A||B|;A可逆时|A⁻¹|=|A|⁻¹;|A*|=|A|^(n-1);特征值λ₁,…,λₙ时|A|=λ₁λ₂…λₙ;若A与B相似,则|A|=|B|。行列式计算方法:化为上下三角行列式、按行/列展开、递推法、数学归纳法、逐行(列)相加等。向量:n维向量概念,加法与数乘运算。线性表示:β可由α₁,…,αₛ线性表出的充要条件是r(α₁,…,αₛ)=r(α₁,…,αₛ,β);向量组等价指两组向量可相互线性表出;若β可由α₁,…,αₛ表出,则r(α₁,…,αₛ)≤r(β₁,…,βₜ)。线性相关:存在不全为0的k₁,…,kₛ使k₁α₁+…+kₛαₛ=0,充要条件是r(α₁,…,αₛ)<s;某αi可由其余向量线性表出,或n+1个n维向量必相关。线性无关:仅当k₁=…=kₛ=0时k₁α₁+…+kₛαₛ=0,充要条件是r(α₁,…,αₛ)=s;任意αi不可由其余向量表出,原无关则延伸组无关,缩短组相关。向量组的秩:极大线性无关组的向量个数,向量组等价则秩相等,矩阵行变换可求极大无关组与秩。向量空间:n维向量空间,基底(线性无关且可表空间任意向量),过渡矩阵,规范正交基(向量正交且模为1),坐标(基底表出系数)。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。